beat365官方网站量子材料科學中心陳昱安助理教授與合作者在量子計算領域取得重要進展。研究團隊提出了一種算法，可以從二維廣義泡利穩定子碼中提取拓撲數據。2024年8月8日，相關成果以“在二維系統中提取廣義泡利穩定子碼的拓撲序”（Extracting topological orders of generalized Pauli stabilizer codes in two dimensions）為題，在線發表于《物理學評論X量子》（PRX Quantum）上。

在迅速發展的量子計算領域，量子碼的魯棒性和多功能性對于構建實用且抗幹擾的系統至關重要。本文介紹了一種新穎的算法，該算法顯著擴展了我們從二維量子系統的廣義泡利穩定子碼中提取和分析拓撲序的能力。這一進展不僅加深了我們的理論理解，也提升了量子糾錯的實際應用，這對構建可靠的量子計算機至關重要。

以往對量子碼的研究通常集中在素數維度的量子比特（qudit），即其限制在有限的環面碼（toric code）上。我們新引入的算法突破了這個限制，成功應用于非素數維度的量子比特上，如圖1（左）所示的六半子穩定子碼（six-semion stabilizer code）。這種擴展的适用性使研究人員能夠探索更廣泛的量子系統，發現以前難以觀察到的拓撲序。并且我們可以通過算法高效地設計和驗證新的量子糾錯碼，如圖1（右）所示的自對偶CSS量子碼。

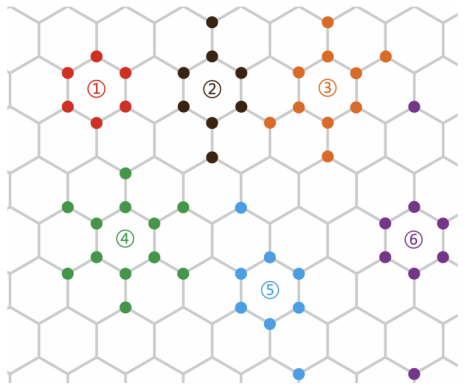
圖1：（左）六半子穩定子碼（Six-semion stabilizer code）。在四邊形晶格上，每條邊上有兩個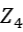的量子比特。（右）六個自對偶CSS量子碼的例子。在六邊形晶格上，每個頂點上有一個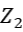的量子比特。例如：第一個是色碼（color code），它由圖中所示模樣的全都是X和全都是Z的兩個穩定子構成。

該算法的核心在于将拓撲序的識别轉換為可管理的計算任務，通過高斯消元、Smith标準形等數學工具，算法可以确定所有的任意子（anyon）及其弦算符（string operator），然後計算它們的融合規則（fusion rule）、拓撲自旋（topological spin）和編織統計（braiding statistic），從而全面解析廣義泡利穩定子碼的拓撲屬性，其流程如圖2所示。

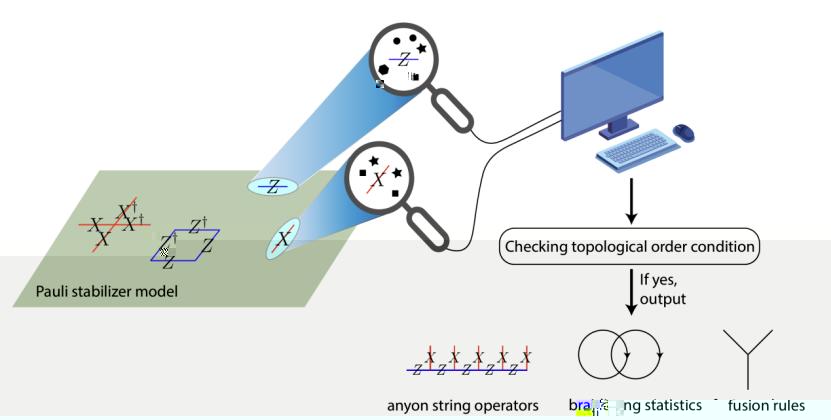
圖2：算法的流程

該研究不僅在理論上有重要突破，還在實際應用上展示了廣泛的前景。随着量子計算技術的進步，理解和利用量子系統的拓撲性質對于發展更強大的量子計算平台至關重要。此項研究工作展示了一種有效的拓撲數據提取方法，在未來的量子技術應用中發揮關鍵作用。

beat365官方网站量子材料科學中心2024級博士生梁子健和馬裡蘭大學的博士生許逸葭為論文的共同第一作者，陳昱安為通訊作者，其他合作者包括馬裡蘭大學的博士生Joseph T. Iosue。

文章鍊接：https://journals.aps.org/prxquantum/abstract/10.1103/PRXQuantum.5.030328